Table of Knot Mosaics - Mosaic Number 6 or Less
|
|||||||
|
The mosaics in this table are color coded with the following key (t = tile number, tm = minimal mosaic tile number):
* Note: Most prime knots that require 32 non-blank tiles to fit on a 6-mosaic (i.e. tm = 32) have tile number less than 32 that can only be achieved on a 7-mosaic. The only knots that have mosaic number 6 and tile number 32 also have crossing number 13, and they are listed at the very bottom of the table. All given mosaics have mosaic number realized. Click "more" to see mosaics with tile number or crossing number realized. |
Click mosaic for larger view.

|
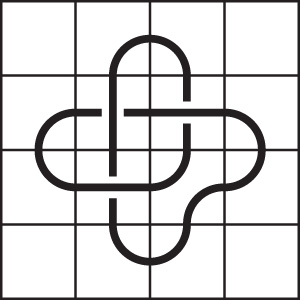
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|

|
|
|

|
|
|
|
|

|
|
|

|
|
|
|

|

|
|

|

|

|
|

|
|
|

|

|

|

|

|

|

|

|
|

|
|

|
|
|
|
|
|

|

|

|

|

|

|
|
|
|

|

|

|

|

|

|

|
|
|
|
|

|

|

|

|

|
|
|

|

|

|

|

|
|

|

|

|

|

|

|
|

|

|
|
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|
|
|
|
|
|

|

|

|

|

|

|

|
|
|
|
|
|
|

|

|

|

|

|

|
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|
|

|

|

|

|

|

|

|
|
|
|
|
|

|

|

|

|

|

|

|

|

|

|

|
|
|
|
|
|
|
|

|

|

|
|
|

|

|

|

|

|

|
|

|

|

|
|

|

|

|

|

|

|
*These knots are listed as 10162‑10166 in Rolfsen due to the Perko Pair. | |||||
|
|
|||||||
|
When listing prime knots with crossing number 11 or more, we use the Dowker-Thistlethwaite name of the knot. See KnotInfo for more information. |
|||||||
All knots with mosaic number 6 and crossing number 11 are given here. None of these have tile number 32. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
All knots with mosaic number 6 and crossing number 12 are given here. None of these have tile number realized. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|||||||
All knots with mosaic number 6 and crossing number 13 are given here. Some of these have tile number 32 realized in the given mosaic. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
References:
Heap, A.; Knowles, D. Tile Number and Space-Efficient Knot Mosaics; J. Knot Theory Ramif. 2018, 27.
Heap, A.; Knowles, D. Space-Efficient Knot Mosaics for Prime Knots with Mosaic Number 6; Involve 2019, 12.
Kuriya, T.; Shehab, O. The Lomonaco–Kauffman Conjecture; J. Knot Theory Ramif. 2014, 23.
Lee, H.; Ludwig, L.; Paat, J.; Peiffer, A. Knot Mosaic Tabulation; Involve 2018, 11.
Lomonaco, S.J.; Kauffman, L.H. Quantum Knots and Mosaics; Quantum Inf. Process. 2008, 7, 85–115.
 : t = 17;
: t = 17; : t = 22;
: t = 22;  : t = 24;
: t = 24;  : t = 27;
: t = 27;  : tm = 32*
: tm = 32*


























































































































































